When the method is applied to the wave equation for arbitrary inhomogeneity and elliptical velocity dependence it involves
My next step is to apply the above method to find the
characteristics of
Cauchy's equations of motion (5) for inhomogeneous anisotropic
media. The characteristic
surface is one on which the second-order derivatives of ![]() cannot
be determined.
The first-order derivatives in equations (5)
are determined from the initial conditions.
cannot
be determined.
The first-order derivatives in equations (5)
are determined from the initial conditions.
According to Bos (2003), the characteristic
surface is one on which the second-order partial derivatives
of ![]() cannot be determined. So let us consider a
surface
cannot be determined. So let us consider a
surface ![]() given in functional form by
given in functional form by
![]() .
We then require initial conditions on
.
We then require initial conditions on ![]() that are
that are
![$\displaystyle \nabla=\left[\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2},
\frac{\partial}{\partial x_3},\frac{\partial}{\partial t}\right] ,$](img28.png)
The twelve first-order derivatives of ![]() are determined
from the initial conditions. I have solved for them
explicitly, but I omit that mathematics here for brevity. I
may include it in my thesis.
As in Bos (2003), the solutions for the first-order derivatives
of
are determined
from the initial conditions. I have solved for them
explicitly, but I omit that mathematics here for brevity. I
may include it in my thesis.
As in Bos (2003), the solutions for the first-order derivatives
of ![]() can be
abbreviated, so that
can be
abbreviated, so that
![$\displaystyle \frac{\partial u_i}{\partial t}[\mathbf{x},f(\mathbf{x})]=\alpha_i(\mathbf{x})$](img31.png) and and![$\displaystyle \qquad \frac{\partial u_i}{\partial x_j}[\mathbf{x},f(\mathbf{x})]=F_{ij}(\mathbf{x}) .$](img32.png) |
(9) |
The above twelve equations (for ![]() )
can then be differentiated with respect to
)
can then be differentiated with respect to
![]() to obtain,
first for terms involving
to obtain,
first for terms involving
![]() , nine scalar equations:
, nine scalar equations:
![$\displaystyle \frac{\partial \mathbf{\alpha}}{\partial x_j}(\mathbf{x})= \frac{...
...athbf{x},f(\mathbf{x})] \frac{\partial \mathbf{f}}{\partial x_j}(\mathbf{x}) .$](img38.png) |
(10) |
![$\displaystyle \mathbf{F}^{[j]}=\frac{\partial \mathbf{u}}{\partial x_j}=
\left[F_{1j},F_{2j},F_{3j}\right] ,
$](img39.png)
![$\displaystyle \frac{\partial \mathbf{F}^{[j]}}{\partial x_k}(\mathbf{x})= \frac...
...athbf{x},f(\mathbf{x})] \frac{\partial \mathbf{f}}{\partial x_k}(\mathbf{x}) .$](img40.png) |
(11) |
For this system of equations not to have a solution
for the second partial derivatives, the determinant
of the thirty-by-thirty matrix of
coefficients of the second partial derivatives
must be zero. This matrix is given in terms of
elasticity-matrix coefficients rather than
elasticity-tensor coefficients in appendix A.
The matrix has 54 entries that are one of (or twice one of) the
21 independent elasticity coefficients or are a sum
of two of them, plus three ![]() 's, plus six
's, plus six ![]() 's, nine
's, nine ![]() 's,
and twelve
's,
and twelve ![]() 's, and 27 ones, so 111
non-zero terms (but only 26 independent components of those terms)
which means 789 zeros. Each
's, and 27 ones, so 111
non-zero terms (but only 26 independent components of those terms)
which means 789 zeros. Each ![]() is
is
![]() .
The components of that thirty-by-thirty matrix depend on components
of the gradient of
.
The components of that thirty-by-thirty matrix depend on components
of the gradient of ![]() and on the elements of the elasticity matrix.
That thirty-by-thirty matrix multiplied by a vector of second-order
derivatives gives the known terms depending on the first-order
derivatives. The determinant of the thirty-by-thirty matrix is given on two pages
in appendix B. When set to zero it is a nonlinear first-order
PDE, an eikonal equation, for
and on the elements of the elasticity matrix.
That thirty-by-thirty matrix multiplied by a vector of second-order
derivatives gives the known terms depending on the first-order
derivatives. The determinant of the thirty-by-thirty matrix is given on two pages
in appendix B. When set to zero it is a nonlinear first-order
PDE, an eikonal equation, for ![]() . The numerical solving
of this equation is one target of my research.
. The numerical solving
of this equation is one target of my research.
As a check, I set the elasticity matrix equal to the isotropic
elasticity matrix in terms of ![]() and
and ![]() and evaluated
the determinant with Mathematica and set it equal to zero to
get
and evaluated
the determinant with Mathematica and set it equal to zero to
get
![$\displaystyle \left\{(\lambda+2\mu)\left[\left(\frac{\partial f}{\partial x_1}\...
...}\right)^2
+\left(\frac{\partial f}{\partial x_3}\right)^2\right]\right\}=0 ,
$](img51.png)
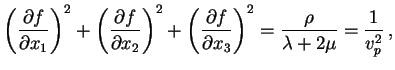 |
(12) |
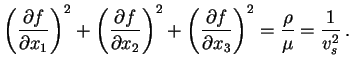 |
(13) |