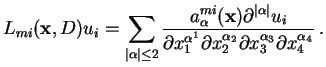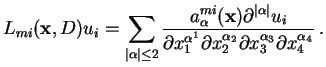Next: Principal symbols and the
Up: Principal symbols, and their
Previous: Principal symbols, and their
Contents
Rauch (1991) says that a smooth hypersurface 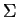 is characteristic
only if the principal symbol
is characteristic
only if the principal symbol
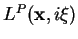 is zero for
is zero for
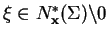 , where
, where
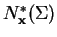 is a 1-D subspace of
is a 1-D subspace of
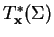 .I have used this principal-symbol method of determining
characteristics to check against the method of
characteristics used in the previous subsection. But in the
case of the system of PDEs (5) the system
is formulated in terms of a matrix operator
.I have used this principal-symbol method of determining
characteristics to check against the method of
characteristics used in the previous subsection. But in the
case of the system of PDEs (5) the system
is formulated in terms of a matrix operator
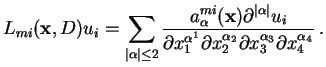 |
(14) |
In that equation 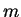 and
and 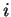 range from one to three and
range from one to three and
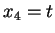 . The procedure of replacing
. The procedure of replacing 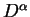 by
by
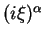 and considering only the highest
order terms,
and considering only the highest
order terms,
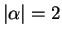 , results in a principal-symbol
matrix
, results in a principal-symbol
matrix
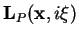 . (I have not included
this matrix here; it is available should readers wish to
see it.) Setting the determinant, given in appendix C,
of this matrix to zero gives a characteristic or eikonal
equation. Again, as in the previous section, it is
a nonlinear first-order equation in the
. (I have not included
this matrix here; it is available should readers wish to
see it.) Setting the determinant, given in appendix C,
of this matrix to zero gives a characteristic or eikonal
equation. Again, as in the previous section, it is
a nonlinear first-order equation in the 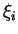 but
is one-fifth as long as the one in the previous section.
However, when the isotropic elasticity matrix
is inserted it reduces to the eikonal equations for
but
is one-fifth as long as the one in the previous section.
However, when the isotropic elasticity matrix
is inserted it reduces to the eikonal equations for
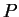 and
and 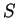 waves as before. Due to the differences
in length of appendix B compared to appendix C
I suspect there
is an error in my Mathematica formulation of the first
case, which I will attempt to trace, despite it reducing
to the correct equations for the isotropic case.
waves as before. Due to the differences
in length of appendix B compared to appendix C
I suspect there
is an error in my Mathematica formulation of the first
case, which I will attempt to trace, despite it reducing
to the correct equations for the isotropic case.




Next: Principal symbols and the
Up: Principal symbols, and their
Previous: Principal symbols, and their
Contents
David Dalton
2004-04-20