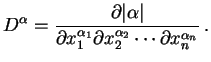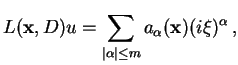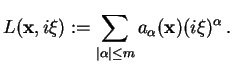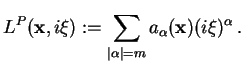Principal symbols, and their application to characteristics

As a preliminary to defining the symbol of a differential operator (Rauch, 1991; Renardy and Rogers, 1992), let me first explain the concept of multi-indices. A multi-index is a vector

$$\alpha=(\alpha_1,\alpha_2,\ldots,\alpha_n)$$

which has components that are non-negative integers. The following definitions also apply:

$$\vert\alpha\vert=\alpha_1+\alpha_2+\cdots+\alpha_n,\qquad \alpha!=\alpha_1!\alpha_2!\ldots\alpha_n! .$$

For vector $\mathbf{x}=(x_1,x_2,\ldots,x_n)$,

$$\mathbf{x}^\alpha=x_1^{\alpha_1}x_2^{\alpha_2}\cdots x_n^{\alpha_n} .$$

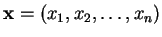Partial derivatives can be written as

$$D^\alpha=\frac{\partial \vert\alpha\vert}{\partial x_1^{\alpha_1} \partial x_2^{\alpha_2}\cdots \partial x_n^{\alpha_n}} .$$

Then, given a linear differential expression of the form

$$L(\mathbf{x},D)u=\sum_{\vert\alpha\vert\leq m} a_{\alpha}(\mathbf{x})(i \mathbf{\xi})^\alpha ,$$

the symbol of that expression is

$$L(\mathbf{x},i\mathbf{\xi}):=\sum_{\vert\alpha\vert\leq m}a_{\alpha}(\mathbf{x}) (i\mathbf{\xi})^\alpha .$$

The principal part of that symbol, also called the principal symbol, is

$$L^P(\mathbf{x},i\mathbf{\xi}):=\sum_{\vert\alpha\vert= m}a_{\alpha}(\mathbf{x}) (i\mathbf{\xi})^\alpha .$$