| (15) |
Both pseudo-differential operators and Fourier-integral operators can make it possible to handle differential operators with variable coefficients in a way similar to that in which one would handle differential operators with constant coefficients using the Fourier transform. However, in the case of equations (5) the coefficients of the partial derivatives, while variable in space due to inhomogeneity, are constant at a given point over time. Thus, the full generality of FIOs is not required, but a simpler variant with constant coefficient can be used. Also equations (5) are a linear system.
For instance, Hörmander (1971) gives the constant coefficient example of the inhomogeneous Laplace equation, an elliptic equation:
| (15) |
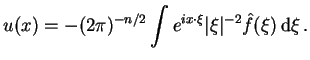 |
(16) |
In a related formulation,
Candès and Demanet (2003) state that an operator ![]() is said to
be a Fourier-integral operator if it is of the form
is said to
be a Fourier-integral operator if it is of the form
While completing the application of the standard method of characteristics and principal-symbol variant, which will involve numerically solving the respective eikonal equations, I plan to read more on FIO theory and applications. The principal-symbol method for finding the characteristic surface required finding the principal symbol matrix of equations (5). This will be useful in my applying FIOs to equations (5) since FIO theory draws on symbols and the Fourier Transform. This FIO analysis will draw on my study of Sobolev spaces, symbols, functional analysis, partial differential equations and pseudo-differential operators in 2003-2004.
One advantage of FIOs is that they allow an elegant description of the propagation of wavefronts. Equations of motion (5) are a complicated though linear system of three partial-differential equations with constant (in time but not space) coefficients. FIO theory is a powerful modern mathematical theory for the analysis of such equations. However, just applying a new mathematical technique for the sake of testing said mathematical technique, while a worthwhile exercise, is not my complete objective. My aim is threefold: to test the new mathematics by application, to reveal subtleties of modelling not apparent in ray theory solution of the eikonal and transport equations, and to show some advantages over full numerical solution.